Kako dokazati da slijed konvergira? Osnovna svojstva konvergentnih sekvenci
Za mnoge ljude matematička analiza samo je zbirka nerazumljivih brojeva, znački i definicija, daleko od stvarnog života. Međutim, svijet u kojemu postojimo izgrađen je na numeričkim obrascima, čija identifikacija pomaže ne samo poznavanju okolnog svijeta i rješavanju složenih problema, već i pojednostavljenju svakodnevnih praktičnih zadataka. Što matematičar znači kad kaže da se numerička sekvencija konvergira? To bi trebalo biti detaljnije raspravljeno.
sadržaj

Što je infinitezimalno?
Zamislite matryoshkas, koji su smješteni jedan u drugu. Njihove dimenzije, napisane u obliku brojeva, počevši od većeg i završavaju s manjom od njih, tvore niz. Ako zamišljate beskonačan broj takvih sjajnih figura, tada će rezultat serija biti fantastično dug. Ovo je konvergentni numerički slijed. I teži nuli, jer veličina svake sljedeće lutke, katastrofalno smanjuje, postupno se pretvara u ništa. Dakle, lako je objasniti: što je beskonačno mali.
Sličan primjer može biti cesta koja se proteže u daljinu. A vizualne dimenzije automobila koji se kreću duž promatrača, postupno se smanjuju, pretvaraju u bezobličnu česticu koja sliči točki. Dakle, stroj, poput objekta, koji se kreće u nepoznatom smjeru, postaje beskonačno malen. Parametri ovog tijela nikada neće biti nuli u doslovnom smislu te riječi, ali uvijek imaju tendenciju da ta vrijednost bude u krajnjoj granici. Stoga ova sekvenca ponovno konvergira na nulu.

Sve izračunavamo po kapi
Zamislite sada svjetovnu situaciju. Liječnik je propisao da uzima lijek, počevši od deset kapi dnevno i dodajući dva u svaki sljedeći dan. I tako je liječnik predložio da se nastavi dok se ne iscrpi sadržaj mjehurića lijekova, čiji volumen iznosi 190 kapi. Iz gore navedenog slijedi da će broj takvih, obojenih u danima, biti sljedeći serijski broj: 10, 12, 14 i tako dalje.
Kako saznati vrijeme cijelog tečaja i broj članova slijeda? Ovdje, naravno, možete brojati kapljice na primitivan način. Ali, to je puno lakše, s obzirom na uzorak, koristiti formulu za sumu od jednog aritmetičkog niza s korakom d = 2. A uz korištenje ove metode kako bi saznali da je broj članova niza brojeva jednak je 10. U ovom slučaju, kao i10 = 28. Broj člana označava broj dana uzimanja lijeka, a 28 odgovara broju kapi koje bi pacijent trebao konzumirati posljednjeg dana. Pridružuje li se ova sekvenca? Ne, jer, unatoč činjenici da je ograničen odozdo za 10, a iznad - 28, takva numerička serija nema ograničenja, za razliku od prethodnih primjera.
Koja je razlika?
Pokušajmo pojasniti: kada se numerička serija ispravi kao konvergentna sekvenca. Definicija takve vrste, kao što se može zaključiti iz gore navedenog, izravno je povezana s pojmom konačnog ograničenja, čija prisutnost otkriva suštinu pitanja. Dakle, koja je temeljna razlika između prethodno spomenutih primjera? I zašto se potonji broj 28 ne može smatrati granicom numeričke serije Xn = 10 + 2 (n-1)?
Da biste pojasnili ovo pitanje, razmotrite drugi slijed naveden dolje navedenom formulom, gdje n pripada skupu prirodnih brojeva.

Ova zajednica članova je skup običnih frakcija, čiji brojnik je 1, a nazivnik stalno raste: 1, frac12- ...
Štoviše, svaki uzastopni predstavnik ove serije na mjestu na brojčanim crtama sve više i više približava 0. I to znači da postoji četvrti u kojem su bodovi dosadno oko nula, što je granica. I što su bliže tome, to je bliža njihova koncentracija na redak brojeva. I udaljenost između njih dramatično se smanjuje, pretvarajući se u infinitezimalno. Ovo je znak da slijed konvergira.

Slično tome, obojeni pravokutnici prikazani na slici, uklonjeni u prostoru, vizualno su složenije, a hipotetska granica postaje zanemariva.
Beskonačno velike sekvence
Nakon što smo analizirali definiciju konvergentne sekvence, sada se obratimo suprotnim primjerima. Mnogi od njih bili su poznati čovjeku od davnih vremena. Najjednostavnije varijante divergentnih sekvenci su niz prirodnih i parnih brojeva. Oni se nazivaju beskonačno velikim na drugi način, budući da njihovi članovi, stalno rastu, sve više približavaju pozitivnom beskonačnosti.
Primjeri takvih također mogu biti bilo koja od aritmetičkih i geometrijskih progresija s korakom i nazivnikom, odnosno veća od nule. Divergentne sekvence smatraju se, pored toga, numeričke serije, koje uopće nisu ograničene. Na primjer, Xn= (-2)n-1.
Fibonacci slijed
Praktična upotreba prethodno spomenutih numeričkih serija za čovječanstvo je neupitna. Ali postoje i mnogi drugi prekrasni primjeri. Jedan od njih je Fibonacciova sekvenca. Svaki od njegovih članova, koji počinju s jedinicom, zbroj je prethodnih. Prva dva njezina predstavnika su 1 i 1. Treći 1 + 1 = 2, četvrti 1 + 2 = 3, peti 2 + 3 = 5. Nadalje, prema istoj logici, slijede brojevi 8, 13, 21 i tako dalje.

Ova serija brojeva povećava na neodređeno vrijeme i ima konačnu granicu. Ali ima još jednu izvanrednu imovinu. Omjer svaki sljedeći prethodnom broju sve bliže u vrijednost 0, 618. Moguće je pojasniti razliku između konvergentnih i divergentnih sljedova, jer ako je broj pisati dobivenog kvocijent, rekao je numerička sustav imaju ograničen rok jednak 0,618.
Slijed Fibonacci koeficijenata
Gornja numerička serija široko se koristi u praktične svrhe za tehničku analizu tržišta. Ali to nije ograničeno na njegove sposobnosti koje su Egipćani i Grci znali i mogli primjenjivati u praksi u davna vremena. To potvrđuju piramide i Parthenon koji su ih izgradili. Doista, broj 0, 618 je konstantni koeficijent dobro poznatog starog zlatnog dijela. Prema tom pravilu, svaki proizvoljni segment može se podijeliti tako da će omjer između njegovih dijelova podudarati s omjerom između većih segmenata i ukupne duljine.
Izrađujemo niz ovih odnosa i pokušamo analizirati taj slijed. Brojčana serija dobivena je kako slijedi: 1- 0.5-0.67-0.6-0.625-0.615-0.619 i tako dalje. Nastavljajući, stoga možemo osigurati da je granica konvergentnog slijeda zaista 0.618. Međutim, potrebno je napomenuti i druga svojstva ovog uzorka. Ovdje se čini da brojke izgledaju razotkrivene, a ni uopće u poretku povećanja ili smanjenja. To znači da ovaj konvergentni slijed nije monoton. O tome zašto je to način da ide dalje.
Monotonija i ograničenja
Članovi numeričke serije s povećanjem broja mogu se jasno smanjiti (ako x1x2x3hellip-> xnhellip-) ili povećati (ako x123

Nakon što zapišete brojeve određene serije, možete primijetiti da bilo koji od njezinih članova, koji se približava neograničenom broju 1, nikada neće premašiti ovu vrijednost. U ovom slučaju govorimo o ograničenosti konvergentne sekvence. To se događa kad god postoji pozitivan broj M, koji je uvijek veći od bilo kojeg od izraza serije u apsolutnoj vrijednosti. Ako numerička serija ima monotoničnost i ima ograničenje, pa stoga konvergira, onda to nužno ima ovo svojstvo. I obrnuto ne mora biti istina. To je naznačeno teoremom o ograničenosti konvergentne sekvence.
Upotreba takvih opažanja u praksi vrlo je korisna. Donosimo konkretan primjer istraživanjem svojstava slijeda Xn = n / n + 1, i dokazati svoju konvergenciju. Činjenica da je monotonično je lako pokazati jer (xn+1 - xn) je pozitivan broj za sve vrijednosti n. Granica sekvence jednaka je broju 1, što znači da su svi uvjeti gornjeg teorema, koji se nazivaju i Weierstrassov teorem, zadovoljeni. Teorem o ograničenosti konvergentne sekvence tvrdi da ako ima ograničenje, onda je u svakom slučaju ograničen. Međutim, dajemo sljedeći primjer. Brojčana serija Xn = (-1)n je ograničen odozdo za -1 i iznad 1. Ali taj slijed nije monoton, nema ograničenja i stoga ne konvergira. To jest, ograničenost ne znači uvijek postojanje granice i konvergencije. Da biste to učinili, potrebno je podudarati donju i gornju granicu, kao u slučaju Fibonacciovih koeficijenata.
Brojevi i zakoni svemira
Najjednostavnije varijante konvergentne i divergentne sekvence su možda numerička serija Xn = n i Xn = 1 / n. Prva od njih je prirodna serija brojeva. Kao što je već spomenuto, to je beskonačno veliko. Drugi konvergentne odsječak je vezan, a članovi najvećom blizu beskonačno malo. Svaki od ovih formula predstavlja jednu stranu višestrukog svemira, pomaže osobi na jeziku brojeva i simbola zamisliti i izračunati nešto nepristupačan, nedostupan za ograničenu percepciju.
Zakoni Svemira, od zanemarive, a završava s nevjerojatno velike, također izražava zlatni omjer 0,618. Znanstvenici vjeruju da je položio temelj suštinu stvari i koristi po prirodi za formiranje njenih dijelova. Već je spomenuto ranije odnos između sljedećih i prethodnih članova Fibonacci nizu, ne završiti ovu demonstraciju nevjerojatna svojstva ove jedinstvene serije. Ako uzmemo u obzir kvocijent prethodnog člana naknadno po jednu, dobili smo broj između 0,5 i 0, 33- 0.4- 0,375- 0,384- 0,380- 0,382 i tako dalje. Zanimljivo je da je ovaj omeđen niz konvergira, nije monoton, ali stav pojedinih članova ekstremnih susjednih brojeva uvijek ispada da je oko 0382, koji se također može koristiti u arhitekturi, tehničke analize i drugim industrijama.

Postoje i drugi zanimljivi koeficijenti serije Fibonacci, svi igraju posebnu ulogu u prirodi, a čovjek ih koristi i za praktične svrhe. Matematičari su sigurni da se svemir razvija prema nekoj vrsti "zlatne spirale", koji se sastoji od tih koeficijenata. Pomoću njih mogu se izračunati mnogi fenomeni koji se javljaju na Zemlji iu prostoru, počevši od rasta broja određenih bakterija i završavanjem kretanjem dalekih kometa. Sličan kod poštuje, kao što se ispostavlja, DNA kod.
Polagano geometrijsko napredovanje
Postoji jedan teorem koji tvrdi jedinstvenost granice konvergentne sekvence. To znači da ne može imati dva ili više granica, što je nesumnjivo važno za pronalaženje njezinih matematičkih obilježja.
Razmotrimo neke slučajeve. Bilo koja serija koja se sastoji od članova aritmetičke napredovanja divergentna je, osim u slučaju nula stupnja. Isto se odnosi i na geometrijsku progresiju, čiji je nazivnik veći od 1. Granice takvih numeričkih serija su "plus" ili "minus" beskonačnosti. Ako je nazivnik manji od -1, tada uopće nema ograničenja. Postoje i druge opcije.
Razmotrite brojčanu seriju koju daje formula Xn = (1/4)n-1. Na prvi pogled lako je shvatiti da je taj konvergentni slijed ograničen, jer se strogo smanjuje i ni na koji način ne može uzeti negativne vrijednosti.
Zapišimo određeni broj njegovih uvjeta za redom.
Ispada: 1 - 0.25 - 0.0625 - 0.015625 - 0.00390625 i tako dalje. Dovoljno je jednostavno izračunati razumjeti brzinu određene geometrijske progresije od nazivnika 0<1 уменьшается. В то время как знаменатель членов неограниченно возрастает, сами они превращаются в бесконечно малое. Это значит, что предел числового ряда равен 0. Данный пример ещё раз демонстрирует ограниченность сходящейся последовательности.

Temeljne sekvence
Francuski znanstvenik Auguste Louis Cauchy pokazao je svijetu mnogo djela vezanih uz matematičku analizu. Dao je definicije pojmovima kao što su diferencijalna, integralna, granica i kontinuitet. Istraživao je i osnovna svojstva konvergentnih sekvenci. Da bismo razumjeli bit svojih ideja, potrebno je generalizirati neke važne detalje.
Na samom početku članka se pokazalo da postoje neke sekvence za koje postoji kvart gdje su točke koje predstavljaju određeni broj članova na broj linija, početi skuchivatsya po podstava sve gušće. Istodobno, udaljenost između njih raste kako se broj sljedećeg predstavnika povećava i postaje beskonačno mali. Tako se ispostavlja da se beskonačni broj predstavnika određene serije grupira u određenom susjedstvu, dok postoji konačan broj predstavnika dane serije. Takve sekvence nazivaju se temeljnim.
Poznati kriterij Cauchy, koji je stvorio francuski matematičar, nedvosmisleno pokazuje da je postojanje takvog svojstva dostatno za dokazivanje da se slijed konvergira. Razgovor je također istinito.
Treba napomenuti da je ovaj zaključak francuskog matematičara najvećim dijelom isključivo teorijski interes. Njegova primjena u praksi se smatra prilično složenim, stoga, kako bi se utvrdila konvergencija serije, mnogo je važnije dokazati postojanje niza konačnih ograničenja. Inače, smatra se divergentnim.
Kod rješavanja problema treba uzeti u obzir i osnovna svojstva konvergentnih sekvenci. Prikazani su u nastavku.

Beskonačne sume
Takav poznati istraživači antike, kao i Arhimeda, Euklida, Eudoks koristi iznos beskonačan broj serije za izračunavanje duljine krivulje, količina svemirskih tijela i oblika. Konkretno, to je na taj način uspjelo otkriti područje paraboličkog segmenta. U tu svrhu upotrijebljen je zbroj numeričke serije geometrijske napredovanja s q = 1/4. Na sličan način, bilo je volumena i područja drugih proizvoljnih oblika. Ova je opcija nazvana metodom "iscrpljenosti". Ideja je bila da je studirao kompleks u obliku tijela bio podijeljen na dijelove, koji su bili likovi s lako mjerljivim parametrima. Zbog toga nije bilo teško izračunati svoja područja i količine, nego su se formirali.

Usput, slični zadaci vrlo su poznati modernim školskim djecom i nalaze se u zadaćama USE-a. Jedinstveni način, koji se nalaze daleko od predaka, danas je najjednostavnija verzija rješenja. Čak i ako su dijelovi na kojima je numerička slika podijeljena, samo dva ili tri, dodavanje njihovih područja još uvijek predstavlja zbroj serije brojeva.
Mnogo kasnije, drevni grčki znanstvenici Leibniz i Newton, na temelju iskustva mudrih prethodnika, naučili su zakone integralnog računanja. Znanje svojstava sekvenci pomoglo im je rješavanju diferencijalnih i algebarskih jednadžbi. Trenutno, teorija serije stvorena naporima mnogih generacija talentiranih znanstvenika daje priliku da riješi veliki broj matematičkih i praktičnih problema. Istraživanje numeričkih sekvenci glavni je zadatak riješen matematičkom analizom od trenutka stvaranja.
 Georg Kantor: Postavite teoriju, životopis i obiteljsku matematiku
Georg Kantor: Postavite teoriju, životopis i obiteljsku matematiku Koji je prirodni broj? Povijest, opseg, svojstva
Koji je prirodni broj? Povijest, opseg, svojstva Pravi brojevi i njihova svojstva
Pravi brojevi i njihova svojstva Osnovni koncept teorije vjerojatnosti. Zakoni teorije vjerojatnosti
Osnovni koncept teorije vjerojatnosti. Zakoni teorije vjerojatnosti Znaš li što znači "racionalno" i koji se brojevi nazivaju racionalnim?
Znaš li što znači "racionalno" i koji se brojevi nazivaju racionalnim?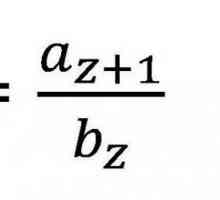 Geometrijska progresija. Primjer s otopinom
Geometrijska progresija. Primjer s otopinom Zlatna sekvenca: princip i značajke
Zlatna sekvenca: princip i značajke Fibonacci slijed. Tako je imenovan po prirodi
Fibonacci slijed. Tako je imenovan po prirodi Definicija, svojstva i vrste algoritama
Definicija, svojstva i vrste algoritama Svojstva matrice i njezine determinante
Svojstva matrice i njezine determinante Što je matematika?
Što je matematika? Geometrijska progresija i njegova svojstva
Geometrijska progresija i njegova svojstva Racionalni brojevi i radnje nad njima
Racionalni brojevi i radnje nad njima Teorija brojeva: teorija i praksa
Teorija brojeva: teorija i praksa Stupnjevi brojeva: povijest, definicija, osnovna svojstva
Stupnjevi brojeva: povijest, definicija, osnovna svojstva Aritmetička progresija
Aritmetička progresija Fibonacci razine u Forex tradingu
Fibonacci razine u Forex tradingu Koristeći PHP funkciju slučajnim
Koristeći PHP funkciju slučajnim Broj PI je matematičko otajstvo
Broj PI je matematičko otajstvo Osnovna pravila diferencijacije koja se koriste u matematici
Osnovna pravila diferencijacije koja se koriste u matematici Numerički slijed: koncept, svojstva, metode dodjele
Numerički slijed: koncept, svojstva, metode dodjele
 Koji je prirodni broj? Povijest, opseg, svojstva
Koji je prirodni broj? Povijest, opseg, svojstva Pravi brojevi i njihova svojstva
Pravi brojevi i njihova svojstva Osnovni koncept teorije vjerojatnosti. Zakoni teorije vjerojatnosti
Osnovni koncept teorije vjerojatnosti. Zakoni teorije vjerojatnosti Znaš li što znači "racionalno" i koji se brojevi nazivaju racionalnim?
Znaš li što znači "racionalno" i koji se brojevi nazivaju racionalnim? Geometrijska progresija. Primjer s otopinom
Geometrijska progresija. Primjer s otopinom Zlatna sekvenca: princip i značajke
Zlatna sekvenca: princip i značajke